Hoffman–Singleton graph
| Hoffman–Singleton graph | |
|---|---|
| Named after | Alan J. Hoffman Robert R. Singleton |
| Vertices | 50 |
| Edges | 175 |
| Radius | 2 |
| Diameter | 2[1] |
| Girth | 5[1] |
| Automorphisms | 252,000 (PSU(3,52):2)[2] |
| Chromatic number | 4 |
| Chromatic index | 7[3] |
| Properties | Strongly regular Symmetric Hamiltonian Integral Cage Moore graph Cayley graph |
In the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters (50,7,0,1).[4] It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is the highest order Moore graph known to exist.[5] Since it is a Moore graph where each vertex has degree 7, and the girth is 5, it is a (7,5)-cage.
Contents |
Construction
A simple direct construction is the following: Take five pentagons Ph and five pentagrams Qi, so that vertex j of Ph is adjacent to vertices j-1,j+1 of Ph and vertex j of Qi is adjacent to vertices j-2,j+2 of Qi. Now join vertex j of Ph to vertex hi+j of Qi. (All indices mod 5.)
Algebraic properties
The automorphism group of the Hoffman-Singleton graph is a group of order 252,000 isomorphic to PΣU(3,52) the semidirect product of the projective special unitary group PSU(3,52) with the cyclic group of order 2 generated by the Frobenius automorphism. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Hoffman-Singleton graph is a symmetric graph. It is also a Cayley graph.
The characteristic polynomial of the Hoffman-Singleton graph is equal to 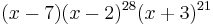 . Therefore the Hoffman-Singleton graph is an integral graph: its spectrum consists entirely of integers.
. Therefore the Hoffman-Singleton graph is an integral graph: its spectrum consists entirely of integers.
Subgraphs
Using only the fact that the Hoffman-Singleton graph is a strongly regular graph with parameters (50,7,0,1), it can be shown that there are 1260 5-cycles contained in the Hoffman-Singleton graph.
Additionally, the Hoffman-Singleton graph contains 525 copies of the Petersen graph.
See also
Notes
- ^ a b Weisstein, Eric W., "Hoffman-Singleton Graph" from MathWorld.
- ^ Hafner, P. R. "The Hoffman-Singleton Graph and Its Automorphisms." J. Algebraic Combin. 18, 7-12, 2003.
- ^ Royle, G. "Re: What is the Edge Chromatic Number of Hoffman-Singleton?" GRAPHNET@istserv.nodak.edu posting. Sept. 28, 2004. [1]
- ^ Brouwer, Andries E., Hoffman-Singleton graph, http://www.win.tue.nl/~aeb/drg/graphs/Hoffman-Singleton.html.
- ^ Hoffman, Alan J.; Singleton, Robert R. (1960), "Moore graphs with diameter 2 and 3", IBM Journal of Research and Development 5 (4): 497–504, MR0140437, http://www.research.ibm.com/journal/rd/045/ibmrd0405H.pdf.
References
- Benson, C. T.; Losey, N. E. (1971), "On a graph of Hoffman and Singleton", Journal of Combinatorial Theory. Series B 11 (1): 67–79, doi:10.1016/0095-8956(71)90015-3, ISSN 0095-8956, MR0281658
- Holton, D.A.; Sheehan, J. (1993), The Petersen graph, Cambridge University Press, pp. 186 and 190, ISBN 0-521-43594-3.